How To Draw Level Curves

Consider the following linear program:

Maximize \(x+y\)

subject to \[\begin{aligned} 2x+3y & \le 5 \\ -2x+ y & \le 1 \\ 3x- y & \le 4 \\ x, y & \ge 0 \end{aligned}\]

We can represent this graphically in the \(xy\)-plane. For each constraint, the set of points \((x,y)\) that satisfies it is a half-plane; the set of points satisfying all of the constraints is then the intersection of all these half planes. In this example it turns out to be a pentagon, shaded red in the image below.

The set of points that satisfy all the constraints is called the feasible region. It is always convex, meaning that whenever two points are in the feasible region, so is the entire line segment connecting them. It doesn't have to be of finite size as it is for this linear program, it can "go off to infinity". It can also be empty! (It is a good exercise to draw half-planes that would give a feasible region of infinite extent, and to draw half-plane that don't have any point common to all, leading to an empty feasible region.)

How can we represent the objective function? The graph of the function would require three dimensions to plot (i.e., the graph is the plane \(z=x+y\) in three-dimensional space). To get something we can draw in the same figure as the feasible region we will instead draw level curves \(x+y = k\) that you get by setting the objective function equal to a constant \(k\). (Since the objective function is linear these level "curves" are actually straight lines.)

Here is a picture of the feasible region together with various level lines for the objective function:

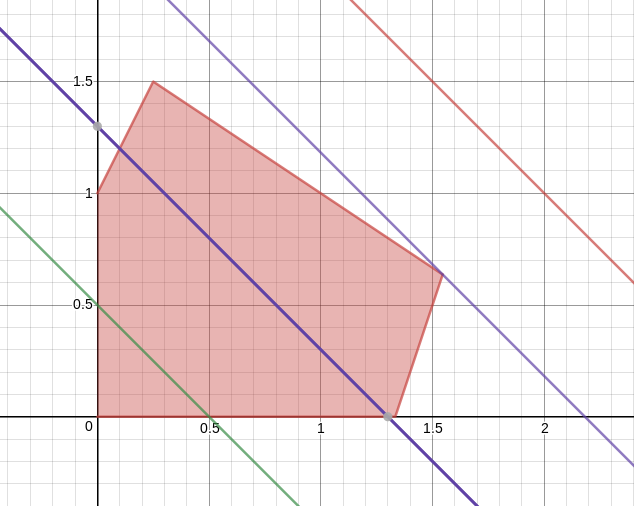
As you change the constant \(k\), the level line slides around, always keeping the same slope. If for some value of \(k\) that line goes through the feasible region, that means that it is possible to obtain the value \(k\) for some choice of \(x\) and \(y\) satisfying the constraints. We want the largest such \(k\), so imagine sliding the line around until it is about to fall off the feasible region: the corresponding \(k\) is the maximum¹ value of the objective function in the feasible region and the answer to the optimization question posed by the linear problem.